Python Fortran Rosetta Stone#
在表达能力和特性方面,Python 与 NumPy 和 Fortran 非常相似。此 Rosetta Stone 展示了如何在两种语言中并排实现许多常见的习惯用法。
如何执行代码片段#
例如,请考虑以下代码片段
在 Python 中,只需将代码保存到文件 example.py 中,并使用 python example.py 执行。在 Fortran 中,将其保存到文件 example.f90 中,并在文件末尾追加行 end(有关此工作原理的更多信息,请参阅 模块 部分)。使用 gfortran example.f90 编译,并使用 ./a.out 执行(当然,您可以向 gfortran 添加编译选项,例如生成具有不同名称的可执行文件)。
数组#
数组是 Fortran 中的内置类型,在 Python 的 NumPy 模块中可用。用法相同,但存在以下差异
Fortran(默认情况下)从 1 开始计数,NumPy 始终从 0 开始
Fortran 数组切片(切片)包含两端,在 NumPy 中,包含起始点,但不包含结束点
在 C 中,数组按行存储在内存中(默认情况下 NumPy 使用 C 存储),而在 Fortran 中,则按列存储(这仅在接下来的两点中重要)
默认情况下,
reshape在 Fortran 中使用 Fortran 顺序,在 NumPy 中使用 C 顺序(在这两种情况下,可选参数order允许使用其他顺序)。这在reshape在其他操作(如展平)中隐式使用时也很重要。第一个索引在 Fortran 中最快,而在 NumPy 中,最后一个索引最快
默认情况下,NumPy 会很好地打印二维数组,而在 Fortran 中,必须指定格式才能打印它(Fortran 也按列打印,因此必须转置数组才能按行打印)
其他所有内容都相同,特别是
NumPy 和 Fortran 数组操作之间存在一对一的对应关系,并且可以在两种语言中轻松/自然地表达相同的事物
对于二维数组,第一个索引是行索引,第二个是列索引(就像在数学中一样)
如果 NumPy 和 Fortran 数组具有相同的形状并且相同的元素对应于相同的索引,则它们是等效的(内部内存存储是什么并不重要)
允许任何涉及数学函数的数组表达式,例如
a**2 + 2*a + exp(a)、sin(a)、a * b和a + b(它按元素进行运算)您需要使用函数来使用矩阵乘法将两个矩阵相乘
高级索引/切片
数组可以是任何整数、实数或复数类型
…
from numpy import array, size, shape, min, max, sum
a = array([1, 2, 3])
print(shape(a))
print(size(a))
print(max(a))
print(min(a))
print(sum(a))
integer :: a(3)
a = [1, 2, 3]
print *, shape(a)
print *, size(a)
print *, maxval(a)
print *, minval(a)
print *, sum(a)
end program
from numpy import reshape
a = reshape([1, 2, 3, 4, 5, 6], (2, 3))
b = reshape([1, 2, 3, 4, 5, 6], (2, 3), order="F")
print(a[0, :])
print(a[1, :])
print()
print(b[0, :])
print(b[1, :])
integer :: a(2, 3), b(2, 3)
a = reshape([1, 2, 3, 4, 5, 6], [2, 3], order=[2, 1])
b = reshape([1, 2, 3, 4, 5, 6], [2, 3])
print *, a(1, :)
print *, a(2, :)
print *
print *, b(1, :)
print *, b(2, :)
end program
[1 2 3]
[4 5 6]
[1 3 5]
[2 4 6]
1 2 3
4 5 6
1 3 5
2 4 6
from numpy import array, size, shape, max, min
a = array([[1, 2, 3], [4, 5, 6]])
print(shape(a))
print(size(a, 0))
print(size(a, 1))
print(max(a))
print(min(a))
print(a[0, 0], a[0, 1], a[0, 2])
print(a[1, 0], a[1, 1], a[1, 2])
print(a)
integer :: a(2, 3)
a = reshape([1, 2, 3, 4, 5, 6], [2, 3], order=[2, 1])
print *, shape(a)
print *, size(a, 1)
print *, size(a, 2)
print *, maxval(a)
print *, minval(a)
print *, a(1, 1), a(1, 2), a(1, 3)
print *, a(2, 1), a(2, 2), a(2, 3)
print "(3i5)", transpose(a)
end program
(2, 3)
2
3
6
1
1 2 3
4 5 6
[[1 2 3]
[4 5 6]]
2 3
2
3
6
1
1 2 3
4 5 6
1 2 3
4 5 6
from numpy import array, all, any
i = array([1, 2, 3])
all(i == [1, 2, 3])
any(i == [2, 2, 3])
integer :: i(3)
i = [1, 2, 3]
all(i == [1, 2, 3])
any(i == [2, 2, 3])
from numpy import array, empty
a = array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
b = empty(10)
b[:] = 0
b[a > 2] = 1
b[a > 5] = a[a > 5] - 3
integer :: a(10), b(10)
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
where (a > 5)
b = a - 3
elsewhere (a > 2)
b = 1
elsewhere
b = 0
end where
end program
from numpy import array, empty
a = array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
b = empty(10)
for i in range(len(a)):
if a[i] > 5:
b[i] = a[i] - 3
elif a[i] > 2:
b[i] = 1
else:
b[i] = 0
integer :: a(10), b(10)
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
where (a > 5)
b = a - 3
elsewhere (a > 2)
b = 1
elsewhere
b = 0
end where
end program
from numpy import array, sum, ones, size
a = array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
print(sum(a))
print(sum(a[(a > 2) & (a < 6)]))
o = ones(size(a), dtype="int")
print(sum(o[(a > 2) & (a < 6)]))
integer :: a(10)
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print *, sum(a)
print *, sum(a, mask=a > 2 .and. a < 6)
print *, count(a > 2 .and. a < 6)
end program
from numpy import array, dot
a = array([[1, 2], [3, 4]])
b = array([[2, 3], [4, 5]])
print(a * b)
print(dot(a, b))
integer :: a(2, 2), b(2, 2)
a = reshape([1, 2, 3, 4], [2, 2], order=[2, 1])
b = reshape([2, 3, 4, 5], [2, 2], order=[2, 1])
print *, a * b
print *, matmul(a, b)
end program
[[ 2 6]
[12 20]]
[[10 13]
[22 29]]
2 12 6 20
10 22 13 29
from numpy import array, pi
a = array([i for i in range(1, 7)])
b = array([(2*i*pi+1)/2 for i in range(1, 7)])
c = array([i for i in range(1, 7) for j in range(1, 4)])
use types, only: dp
use constants, only: pi
integer :: a(6), c(18)
real(dp) :: b(6)
integer :: i, j
a = [ (i, i = 1, 6) ]
b = [ ((2*i*pi+1)/2, i = 1, 6) ]
c = [ ((i, j = 1, 3), i = 1, 6) ]
一些索引示例#
前 n 个元素
后 n 个元素
选择索引 i 和 j 之间的元素(包括 i 和 j)
选择从索引 i 开始的 n 个元素
选择 -n 到 n 之间的元素
(包括 -n 和 n)
遍历整个数组
循环遍历第 3 个到第 7 个元素(包括第 3 个和第 7 个)
将字符串在索引 i 和 j 处拆分为三个部分,这些部分为
拉普拉斯更新
模块#
Fortran 和 Python 导入语句的比较
以下 Python 语句在 Fortran 中没有等效项
Fortran 模块的工作方式与 Python 模块相同。差异
Fortran 模块不能嵌套(即它们都是顶级模块,而在 Python 中,可以使用
__init__.py文件任意嵌套模块)Python 中的
import A在 Fortran 中没有等价的功能。可以在 Fortran 中指定私有模块符号。
相同的功能
一个模块包含变量、类型和函数/子程序。
默认情况下,所有变量/类型/函数都可以从其他模块访问,但可以通过显式指定哪些符号是私有的或公有的来更改此行为(在 Python 中,这只适用于隐式导入)。
公共符号不会污染全局命名空间,但需要从模块中显式导入才能使用它们。
将符号导入模块成为该模块的一部分,然后可以从其他模块导入。
可以使用显式或隐式导入(推荐使用显式导入)。
创建模块
并从主程序中使用它,如下所示
在 Fortran 中,可以省略 program main 行,也可以只用 end 而不是 end program 结束文件。这样,只需在代码片段末尾添加 end 即可测试任何代码片段。
为了指定哪些符号是公共的和私有的,可以使用
__all__ = ["i", "f"]
i = 5
def f(x):
return x + 5
def g(x):
return x - 5
module a
implicit none
private
public i, f
integer :: i = 5
contains
integer function f(x) result(r)
integer, intent(in) :: x
r = x + 5
end function
integer function g(x) result(r)
integer, intent(in) :: x
r = x - 5
end function
end module
不过存在差异。在 Fortran 中,符号 g 将是私有的(无论使用显式或隐式导入,都无法从其他模块导入),f 和 i 是公共的。在 Python 中,当使用隐式导入时,不会导入符号 g,但当使用显式导入时,仍然可以导入符号 g。
浮点数#
NumPy 和 Fortran 都可以处理任何指定的精度,如果未指定精度,则使用默认的平台精度。
在 Python 中,默认精度通常是双精度,而在 Fortran 中是单精度。另请参见相关的 Python 和 NumPy 文档。
在 Fortran 中,习惯上始终使用 _dp 后缀指定精度,其中 dp 在下面的 types.f90 模块中定义为 integer, parameter :: dp=kind(0.d0)(以便可以在需要时在一个地方更改精度)。如果未指定精度,则使用单精度(因此,这会导致单/双精度损坏),因此*始终*需要指定精度。
在下面所有 Fortran 代码片段中,假设您已执行 use types, only: dp。 types.f90 模块为
module types
implicit none
private
public dp, hp
integer, parameter :: dp=kind(0.d0), & ! double precision
hp=selected_real_kind(15) ! high precision
end module
数学和复数#
Fortran 具有内置的数学函数,在 Python 中,必须从 math 模块或(对于更高级的函数)从 SciPy 包中导入它们。Fortran 不包含常量,因此必须使用 constants.f90 模块(包含在下面)。
否则用法相同。
Fortran 模块 constants.f90
module constants
use types, only: dp
implicit none
private
public pi, e, I
! Constants contain more digits than double precision, so that
! they are rounded correctly:
real(dp), parameter :: pi = 3.1415926535897932384626433832795_dp
real(dp), parameter :: e = 2.7182818284590452353602874713527_dp
complex(dp), parameter :: I = (0, 1)
end module
字符串和格式化#
Python 和 Fortran 的功能几乎等效,只有语法略有不同。
在 Python 和 Fortran 中,字符串都可以用 " 或 ' 分隔。
有三种通用的方法可以打印格式化字符串
print("Integer", 5, "and float", 5.5, "works fine.")
print("Integer " + str(5) + " and float " + str(5.5) + ".")
print("Integer %d and float %f." % (5, 5.5))
use utils, only: str
print *, "Integer", 5, "and float", 5.5, "works fine."
print *, "Integer " // str(5) // " and float " // str(5.5_dp) // "."
print '("Integer ", i0, " and float ", f0.6, ".")', 5, 5.5
以下是一些常用的格式
嵌套函数#
Python 和 Fortran 都允许嵌套函数访问外部函数的命名空间。
使用方法如下
可以在回调中使用嵌套函数传递上下文
def simpson(f, a, b):
return (b-a) / 6 * (f(a) + 4*f((a+b)/2) + f(b))
def foo(a, k):
def f(x):
return a*sin(k*x)
print(simpson(f, 0., pi))
print(simpson(f, 0., 2*pi))
real(dp) function simpson(f, a, b) result(s)
real(dp), intent(in) :: a, b
interface
real(dp) function f(x)
use types, only: dp
implicit none
real(dp), intent(in) :: x
end function
end interface
s = (b-a) / 6 * (f(a) + 4*f((a+b)/2) + f(b))
end function
subroutine foo(a, k)
real(dp) :: a, k
print *, simpson(f, 0._dp, pi)
print *, simpson(f, 0._dp, 2*pi)
contains
real(dp) function f(x) result(y)
real(dp), intent(in) :: x
y = a*sin(k*x)
end function f
end subroutine foo
使用方法如下
循环中的控制流#
Python 和 Fortran 中常见的循环类型分别是 for 和 do 循环。在这两种语言中,都可以跳过单个循环或停止循环的执行,但执行此操作的语句有所不同。
break 和 exit 语句#
在 Python 中,break 用于停止最内层循环的执行。在 Fortran 中,这是通过 exit 语句完成的。对于命名循环,可以通过将循环名称附加到 exit 语句来指定受影响的循环。否则,将中断最内层循环。
Python 的 exit() 中断程序或交互式会话的执行。
continue 和 cycle 语句#
Python 的 continue 语句用于跳过循环体中的其余部分。然后循环在下一个迭代周期继续。Fortran 的 continue 语句不执行任何操作,应使用 cycle 代替。对于命名循环,可以通过将循环名称附加到 cycle 语句来指定受影响的循环。
示例#
Mandelbrot 集#
这是一个用 NumPy 编写的真实世界程序,并翻译成 Fortran。
import numpy as np
ITERATIONS = 100
DENSITY = 1000
x_min, x_max = -2.68, 1.32
y_min, y_max = -1.5, 1.5
x, y = np.meshgrid(np.linspace(x_min, x_max, DENSITY),
np.linspace(y_min, y_max, DENSITY))
c = x + 1j*y
z = c.copy()
fractal = np.zeros(z.shape, dtype=np.uint8) + 255
for n in range(ITERATIONS):
print("Iteration %d" % n)
mask = abs(z) <= 10
z[mask] *= z[mask]
z[mask] += c[mask]
fractal[(fractal == 255) & (~mask)] = 254. * n / ITERATIONS
print("Saving...")
np.savetxt("fractal.dat", np.log(fractal))
np.savetxt("coord.dat", [x_min, x_max, y_min, y_max])
program Mandelbrot
use types, only: dp
use constants, only: I
use utils, only: savetxt, linspace, meshgrid
implicit none
integer, parameter :: ITERATIONS = 100
integer, parameter :: DENSITY = 1000
real(dp) :: x_min, x_max, y_min, y_max
real(dp), dimension(DENSITY, DENSITY) :: x, y
complex(dp), dimension(DENSITY, DENSITY) :: c, z
integer, dimension(DENSITY, DENSITY) :: fractal
integer :: n
x_min = -2.68_dp
x_max = 1.32_dp
y_min = -1.5_dp
y_max = 1.5_dp
call meshgrid(linspace(x_min, x_max, DENSITY), &
linspace(y_min, y_max, DENSITY), x, y)
c = x + I*y
z = c
fractal = 255
do n = 1, ITERATIONS
print "('Iteration ', i0)", n
where (abs(z) <= 10) z = z**2 + c
where (fractal == 255 .and. abs(z) > 10) fractal = 254 * (n-1) / ITERATIONS
end do
print *, "Saving..."
call savetxt("fractal.dat", log(real(fractal, dp)))
call savetxt("coord.dat", reshape([x_min, x_max, y_min, y_max], [4, 1]))
end program
要运行 Python 版本,您需要 Python 和 NumPy。要运行 Fortran 版本,您需要来自 Fortran-utils 包的 types.f90、constants.f90 和 utils.f90。这两个版本都会生成等效的 fractal.dat 和 coord.dat 文件。
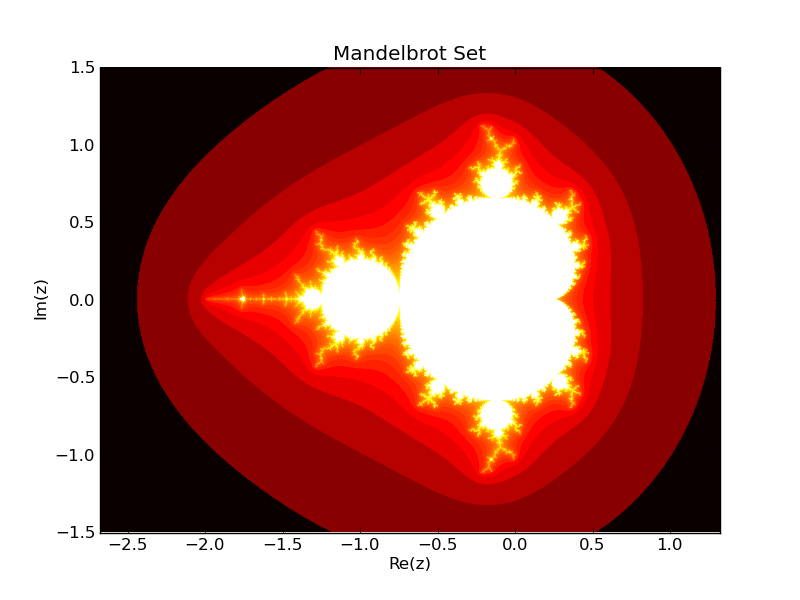
生成的碎形可以通过以下方式查看(您需要 matplotlib)
from numpy import loadtxt
import matplotlib.pyplot as plt
fractal = loadtxt("fractal.dat")
x_min, x_max, y_min, y_max = loadtxt("coord.dat")
plt.imshow(fractal, cmap=plt.cm.hot,
extent=(x_min, x_max, y_min, y_max))
plt.title('Mandelbrot Set')
plt.xlabel('Re(z)')
plt.ylabel('Im(z)')
plt.savefig("mandelbrot.png")
在配备 gFortran 4.6.1 的 Acer 1830T 上的计时结果为
Python |
Fortran |
加速比 |
|
|---|---|---|---|
计算 |
12.749 |
00.784 |
16.3 倍 |
保存 |
01.904 |
01.456 |
1.3 倍 |
总计 |
14.653 |
02.240 |
6.5 倍 |
最小二乘拟合#
在 Python 中,我们通过 SciPy 使用 Minpack,在 Fortran 中,我们直接使用 Minpack。我们首先创建一个名为 find_fit_module 的模块,其中包含一个名为 find_fit 的函数。
from numpy import array
from scipy.optimize import leastsq
def find_fit(data_x, data_y, expr, pars):
data_x = array(data_x)
data_y = array(data_y)
def fcn(x):
return data_y - expr(data_x, x)
x, ier = leastsq(fcn, pars)
if (ier != 1):
raise Exception("Failed to converge.")
return x
module find_fit_module
use minpack, only: lmdif1
use types, only: dp
implicit none
private
public find_fit
contains
subroutine find_fit(data_x, data_y, expr, pars)
real(dp), intent(in) :: data_x(:), data_y(:)
interface
function expr(x, pars) result(y)
use types, only: dp
implicit none
real(dp), intent(in) :: x(:), pars(:)
real(dp) :: y(size(x))
end function
end interface
real(dp), intent(inout) :: pars(:)
real(dp) :: tol, fvec(size(data_x))
integer :: iwa(size(pars)), info, m, n
real(dp), allocatable :: wa(:)
tol = sqrt(epsilon(1._dp))
m = size(fvec)
n = size(pars)
allocate(wa(m*n + 5*n + m))
call lmdif1(fcn, m, n, pars, fvec, tol, info, iwa, wa, size(wa))
if (info /= 1) stop "failed to converge"
contains
subroutine fcn(m, n, x, fvec, iflag)
integer, intent(in) :: m, n, iflag
real(dp), intent(in) :: x(n)
real(dp), intent(out) :: fvec(m)
! Suppress compiler warning:
fvec(1) = iflag
fvec = data_y - expr(data_x, x)
end subroutine
end subroutine
end module
然后我们使用它来寻找一个形如 a*x*log(b + c*x) 的非线性拟合,用于素数列表。
from numpy import size, log
from find_fit_module import find_fit
def expression(x, pars):
a, b, c = pars
return a*x*log(b + c*x)
y = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,
37, 41, 43, 47, 53, 59, 61, 67, 71]
pars = [1., 1., 1.]
pars = find_fit(range(1, size(y)+1), y, expression, pars)
print(pars)
program example_primes
use find_fit_module, only: find_fit
use types, only: dp
implicit none
real(dp) :: pars(3)
real(dp), parameter :: y(*) = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, &
37, 41, 43, 47, 53, 59, 61, 67, 71]
integer :: i
pars = [1._dp, 1._dp, 1._dp]
call find_fit([(real(i, dp), i=1,size(y))], y, expression, pars)
print *, pars
contains
function expression(x, pars) result(y)
real(dp), intent(in) :: x(:), pars(:)
real(dp) :: y(size(x))
real(dp) :: a, b, c
a = pars(1)
b = pars(2)
c = pars(3)
y = a*x*log(b + c*x)
end function
end program
这将打印:
1.4207732655565537 1.6556111085593115 0.53462502018670921